

Up: Main body of lecture 30: Plasma propulsion
Previous: Main body of lecture 30: Plasma propulsion
Derivation of the Debye length
- In the electrostatic approximation, consider a distribution of electrons
that is immersed in a uniform background of positive ions and is in thermal
equilibrium with a potential
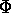 . The density distribution is then a Boltzmann distribution
. The density distribution is then a Boltzmann distribution
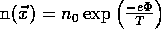
- Imagine a test particle of charge Ze placed at the origin. Poisson's equation is then
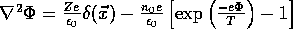
where
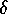 is the Dirac delta function.
is the Dirac delta function.
- For
 , the exponential can be expanded to give
, the exponential can be expanded to give
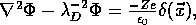
- The Debye length has been introduced.

- The spherically symmetric solution is
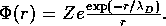
John F Santarius
Fri Apr 19 23:02:29 CDT 1996
