NEEP602 Course Notes (Fall 1996)
Resources from Space
Star and Planet Formation
| 31 Jan. - 5 Feb. 1996 | NEEP 602 | Ed Churchwell |
Microsoft Word and PostScript versions of these notes are also available
I. OVERVIEW: INITIAL CONDITIONS
Where are stars formed?
In molecular clouds--cold, neutral, molecular gas and dust clouds
Evidence: All stars in the process of forming are observed in molecular clouds
All very young star clusters are found in or near molecular clouds.
What do molecular clouds look like?
Opaque at UV and visible wavelengths.
Bright and luminous at infrared wavelengths.
Bright rotational and vibrational molecular emission lines at radio and infrared wavelengths.
3-slides of mol. clouds or "dark clouds"
What are the properties of molecular clouds?
They are cold: 8<= Tkin<=20 K Typical value ~10 K
Low ionization: fe =ne/n ~10-6 - 10-7 => very neutral!
High density: n(H2) >= 103 cm-3
Giant molecular clouds are very massive: M~ 104 to 106 solar masses
Giant molecular clouds are large: Diameters ~ 325 ly
They are clumpy
Supersonic gas motions are found in almost all clouds
Line widths ~ 0.5 to 2 km s-1; sound speed ~ 0.2 km s-1
indicative of nonthermal motions such as rotation, turbulence, shocks, contraction or expansion, stellar bipolar outflows, etc.
What are the conditions that favor the initiation of star formation?
Decrease internal pressure: By decreasing the tempeature or the density or both
Increasing the mean mass per particle by transforming from an atomic gas to a molecular gas.
Decrease the ionization fraction, fe = ne/n to < 10-7 => gas decouples from any
magnetic field present so that magnetic pressure cannot support the cloud.
Increase the external pressure: By partially focused shocks. [3-slides M17]
By ionization of the gas around a molecular clump. [4-slides-Bok Globules, Eagle Neb.]
Low temp | These are all properties that favor star formation as High density | we will show. Molecular clouds have the Low fe | the "right stuff" for star formation. Molecules are Large Mass | very efficient coolants, so it is very hard for such Clumpy structure | clouds to reach temperatures much in excess of ~20 K.
Stars form deep in molecular clouds and as a result are hidden from optical and UV observations, but they can be studied at radio and infrared wavelengths.
What are the systematic properties of the solar system that any successful theory of formation must satisactorily explain?
1. Coplanar orbits of the planets
2. All planets have prograde revolution
3. The revolution of rings and natural moons are all prograde (some moons of the outer planets are not prograde, but these are believed to be captured satellites)
4. All planets except Venus and Uranus have prograde rotation
5. The sun contains all the mass
6. The planets (especially Jupiter and Saturn) contain most of the angular momentum in the solar system
7. Small, dense, iron and silicate rich planets in the inner 2 AU
Slow rotors, few or no moons, no rings, differentiated (molten interiors)
8. Large, low density, gaseous planets rich in H, He and volatile elements at >= 5 AU
Rapid rotors, many moons, all have ring systems
9. Abundance gradient
Inner solar system is poor in light volatile gases such as H, He, but rich in Fe&Ni
Outer solar system is rich in volatiles H, He, etc. Abundances similar to that of the sun.
II. THE PHYSICS OF STAR FORMATION
A. Hydrostatic Equilibrium
For a cloud to be stable against collapse or expansion, its internal pressure must exactly balance gravity at all positions in the cloud. This is called hydrostatic equilibrium. The conditions of hydrostatic equilibrium can be derived as follows:
Consider a small volume in a static spherical gas cloud of mass M and uniform density [[rho]].
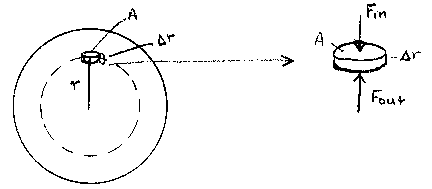
The inward force on the disk is produced only by gravity, so
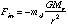
where Mr is the mass interior to radius r and md=A[[Delta]]r[[rho]] is the mass of the disk.
The outward force is simply the internal gas pressure, so
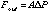
where [[Delta]]P is the force/unit area on the face of the disk.
For equilibrium, we require that
Fout = Fin
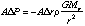
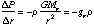
where the acceleration of gravity at position r is
.
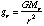Thus, the pressure gradient is balanced by gravity at all points as
required by hydrostatic equilibrium.
In this treatment, we have neglected effects of rotation, magnetic fields, and bulk motions.
Since gr is always radial, hydrostatic equilibrium in gaseous and fluid objects produce spherical shapes.
B. Gravitational Potential Energy and Kinetic Energy of a Sphere
For systems with a large number of particles such as a molecular cloud, we will think in terms of a fluid with density [[rho]] rather than try to deal with many individual particles (atoms or molecules).
In a sphere of constant density [[rho]], the mass M and radius R are related by
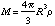
The gravitational potential energy is equivalent to the work required to bring all the matter M from infinity to the final radius R. To calculate the gravitational potential energy U, we will assemble the sphere one thin shell at a time and add them together.
Consider the shell of thickness dr at radius r.
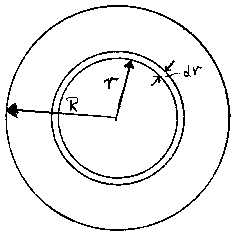
The volume of the shell is
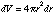
and the mass of the shell is
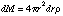
The total mass interior to r is:
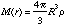
if [[rho]] is constant.
The gravitational potential between any two points separated by distance r is:
U = -Gm1m2/r
The work required to add the mass dM to M(r) is:
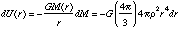
Thus the total work required to assemble the entire sphere is:
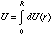
Other shapes will have a different coefficient than 3/5, but all do not
deviate by much from unity. This derivation assumes that the density is
constant with radius. Real clouds will have density that varies with radius,
in many cases it will vary as
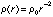
The thermal energy per particle in a gas cloud is:
where N is the total number of particles in the cloud. If u is the mean mass per particle, then N=M/u and
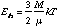
C. Collapsing Clouds
The condition for a cloud to be gravitationally bound is that the gravitational potential U must exceed the internal thermal energy. This implies that the total energy is negative. That is:
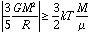
Which implies that
Recall that M and R are not independent since they are related via the density
relation:
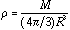
D. The Jeans Criteria
Let us now try to estimate the smallest cloud of a given density [[rho]], mean mass per particle u, and temperature T for which the gravitational and kinetic energies are just equal, that is the point at which the cloud is just balanced between gravity and thermal energy. Note: we neglect turbulent motions, rotation, magnetic pressure, and other bulk motions, thus the equilibrium radius that we derive here will be a lower limit. In practice, the radius that we derive is probably a factor or 2 or more under estimated.
We have in our idealized case:
=>
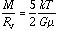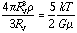
where RJ is the Jeans Radius or the radius at which Eth and U are equal.
Solving for RJ:
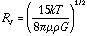
Note:
,
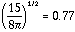which is close to unity. This coefficient will be different for different
geometries but is always close to unity. We will, therefore, write:
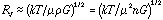where n=[[rho]]/u is the number density.
This is the minimum radius for which a cloud will be just stable for
the given T, [[rho]], and u. Note:
,
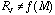so it says nothing about the cloud mass.
As an example, for a cloud with initial density n=103
cm-3, u=2.25 x1.67x10-24 gm, and T=10 K,
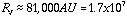solar radii!
It is often convenient to express the M/R relation in terms of the minimum mass or Jeans Mass MJ for which a cloud of [[rho]], u, and T will be just gravitationally stable. This can be done as follows:
=
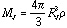
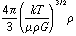
or in terms of gas density n=[[rho]]/u,
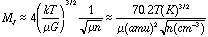
For example, a typical cloud with n=103 cm-3, u=2.25
amu, and T=10 K will have a Jeans mass of
solar masses. A mass much greater than this will be unstable and collapse
under its own gravity.
To form a one solar mass star, the cloud would have to have a density of about 105 cm-3, or a combination of a lower T and higher u and [[rho]].
Caption
Gaseous Pillars in M16 - Eagle Nebula
OH of EGGS as one example of how stars could be initiated into formation
slides of Bok Globules in the Rosette and other nebulae
3 slides of M17 to illustrate partially focused shocks to induce star formation.
an OH to schematically illustrate shock induced star formation
E. Free-Fall Time Scale
Once a cloud becomes gravitationally bound, it will begin to collapse. We now want to estimate how long it will take to collapse to stellar size if umimpeded by other forces.
The acceleration of a particle at radius r is:
or
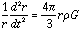
Solving this equation of motion for the time which we will call tff, gives the Free- Fall time:
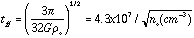yr
where [[rho]]o and no are the initial mass density and number density, respectively. Note that the free-fall time depends only on the initial density and not the cloud mass. It is also independent of the starting radius.
For example, our standard cloud with no = 103 cm-3, T-10 K, and u=2.25 amu
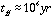or 105 yr for no = 105 cm-3 and all other
parameters unchanged.
Since tff is independent of the starting radius, all matter in a constant density cloud has the same free-fall time. However, as collapse proceeds, the density will increase faster in the inner part of the cloud than in the outer part. This means that tff will decrease from the outer to the inner part of the cloud. This leads to the "inside out" collapse phenomenon in which a small dense core will form while the outer layers are still slowly falling freely toward the center. Although colapse is accelerated at the center (thus reducing tff for the inner layers), the over-all collapse time is about the same as that predicted by the initial density [[rho]]o because most of the time is spent for the outer layers to reach the central core.
How does density change as collapse proceeds from an initially constant density cloud?
We have initially:
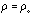and r=ro at t=to. At some later time t when r<ro, we will have
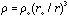
or
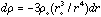
which implies that the fractional change of density with a fractional change of radius is
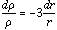
Thus the fractional density increases a factor of three times faster than the fractional radius decreases. This implies that the smaller the initial sphere, the faster its density will grow.
So we see that as the density near the center of the cloud increases, the free- fall time decreases which implies that material near the center falls faster toward the center than material further out. This builds up a strong concentration of matter at the center, which will eventually become the star with an external halo of matter in slow free-fall toward the center.
F. Angular Momentum
If the initial cloud out of which a star formed has any small amount of net angular momentum, as any real cloud will surely have (due to galactic rotational shear, and other bulk motions), then this will be conserved as collapse proceeds. The angular momentum is given by:
L =I[[omega]]
where I is the moment of inertia and [[omega]] is the angular speed of the cloud. For a sphere:
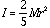and
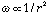
If Io and [[omega]][[omicron]] are the initial values, then
Io [[omega]][[omicron]] = I [[omega]] at any other time from the conservation of L. From which we infer that
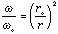
So what does this imply for a collapsing cloud? In this case, the radial acceleration of a test particle of mass m at radius r will have two components
1) gravity:
which directed radially toward the center, and
2) a centripetal term
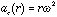directed away from the axis of rotation. The radial
component of
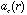is
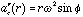
where
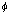is the angle from the axis if rotation to the particle as seen from the center
(see the drawing below).
Thus the net radial acceleration is:
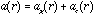
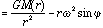
This shows that a(r) is smaller for a rotating cloud than for a non-rotating
cloud. Further, at the pole (
),
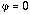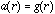only, but at the equator (
)
.
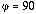Now let's look at the dependence on r of ag and ac for matter in the
equatorial plane where both accelerations are radial. Assume that the mass
interior to our contracting mass point is constant (i.e.
)
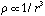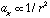
and
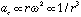since
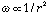
Thus as r decreases, ac increases faster than ag and as contraction proceeds, at some point ac will become equal to and then larger than ag. At the point whereac = ag, the gas cannot contract any closer to the center! Contraction can continue out of the equatorial disk, but not in the disk.
By how much does the cloud contract before ac = ag ?
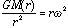
so,
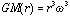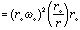but
but
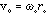
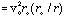
Solving for r/ro:
Note: vo is an orbital velocity and is < vcir(r) if have vr comp
This is the fraction by which the cloud contracts before ac = ag.
Example: For a cloud of T=10 K, n = 104 cm-3, and u=2.25 amu we have:
RJ = 5.7 x 1017 cm; MJ ~ 11 solar masses
If we assume that vo =0.7 vcir(ro) [has to be less that the circular velocity at r0 otherwise there could be no inward motion], then we find:
r/ro ~ 0.5 => the cloud cannot contract anywhere near enough to achieve the factor of ~107 required to form the star.
It is the interplay between centripetal acceleration and gravitational acceleration that causes a collapsing cloud core to form an accretion disk since ac acts perpendicular to the rotation axis and ag acts radially. So we get a structure like that shown schematically below.
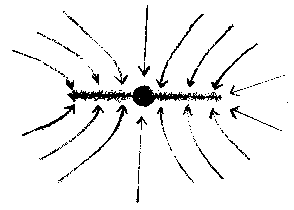
Flow parallel to the rotation axis occurs unimpeded by rotation. Flow toward the center near the equatorial plane is stopped rather quickly by rotation.
FRAGMENTATION
As collapse proceeds an initially large, massive cloud will flatten around the equatorial plane. Ultimately, essentially all matter falles into the plane (except along the polar axis). Matter in the equatorial disk (accretion disk) can contract only so far until it is stopped by rotation. At this point, the cloud is likely to fragment into smaller pieces of higher density. These fragments can then contract further until they reach their centripetal barrier and fragment yet further. The angular momentum goes into orbital motion leaving the fragment left behind to contract further. This process probably continues until fragments of about Jeans mass and radius are formed, at which point the process of star formation can take
place. This is why most stars are formed as part of a star cluster rather than as individual isolated stars.
BIPOLAR JETS AND MOLECULAR OUTFLOWS
To form a star even from a clump of Jeans mass and length, we have shown that
the clump must contract from
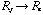which represents a reduction in size by about a factor of 107.
This represents an increase in angular velocity of
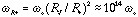
If angular momentum were strickly conserved in the contracting cloud, the resulting star would have a rotation period < 1 sec and an equatorial rotation velocity greater than the speed of light. In fact, the Sun's rotation period is about a month. How did this happen?
The basic question is how does a proto-star shed angular momentum? Throw matter outward! Proto-stars manage to do this, according to the best recent observations and theory, by forming a jet of high speed particles outward along the rotation axis. Paradoxically, as the star is being formed by accretion of matter from an accretion disk, they are at the same time spraying matter outward at high speeds in a jet along the rotation axis. The physics of exactly how this happens is not fully understood, although there are several theories on how this occurs. All theories rely on magnetic fields associated with the star or the disk. We know that this happens, however, because we see the outflowing matter.
Slides and OHs: evidence for disks and jets
associated with young stars
As mass is thrown out (at the expense of rotation), rotation slows and allows mass to flow inward in the accretion disk. This is the only option for the star to grow since the flow out the poles prevent accretion from these directions.
G. ACCRETION LUMINOSITY
The cloud core that forms at the center of a collapsing cloud can become quite luminous in the IR eventhough there are no nuclear reactions to sustain any luminosity. Where does this energy come from? Basically for the conversion of gravitational potential energy to thermal energy. This happens in two ways; 1) the conversion of grav. energy to heat by accelerating in-falling particles, and 2) shock heating as the in-falling particles hit the surface of the cloud core at supersonic speeds. To understand this, we will use the virial theorem.
The virial theorem says that:
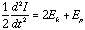
where I is the moment of inertia of the cloud, Ek is the kinetic energy, and
Ep is the potential energy of the cloud. For a cloud core which is almost
stopped contracting and its internal pressure is sufficient to support it
(i.e. it is in equilibrium),
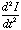~0
and
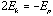
The total energy of the cloud is:
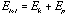
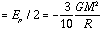
Thus:
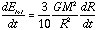
and
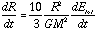which implies that
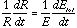
This implies that in any time interval dt, the fractional change in energy dE/E is equal to the fractional change of radius dR/R. The consequence of this is that the rate of collapse can be limited by the rate at which energy can be radiated away.
As a cloud collapses we have
The thermal energy is converted to IR radiation and lost to the star. The high speed particles falling onto the cloud core cause shocks that heat the gas to high temps. and produce high luminosity.
The brightness of the core becomes:
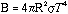where T and R are the temperature and radius of the core.
The luminosity of the core due to in-fall of matter (shock luminosity) is:
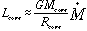where
is the rate of mass in-fall.
For a one solar mass protostar that has collapsed to 500 Ro:
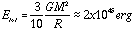
If this energy is released during the last 100 yr of the collapse, then the average luminosity of the core would be
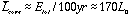
H. EVOLUTION OF A PROTOSTAR
We can identify three distinct pahses of star formation and evolution.
1. Isothermal collapse
Collapse at the free-fall rate
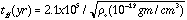It is isothermal because the cloud cannot heat up since the cloud is
transparent to IR radiation due to low density.
The cloud will continue collapsing until an opaque core with an accretion disk forms.
2. The accretion phase
The core grows in mass via accretion from the disk which is fed by in-fall over a larger volume of ambient cloud. The core is opaque and is hot enough that internal pressure almost balances the gravity. As matter is added, the core continues to shrink, but much more slowly at the "Kelvin-Helmholtz" rate:
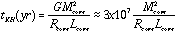
So we have a slowly contracting core on time scales of 107 yr, surrounded by an in-falling envelope on a time scale of ~105 yr.
Once the core achieves a mass >= 80 that of Jupiter, the density and temperature at the center of the core become high enough to sustain nuclear burning and the process of converting 4H => He4 begins. That is the core becomes a star surrounded by a massive accretion disk.
Slide or OH to illustrate
3. Planet formation
Numerical models of the remnant accretion disk evolution after the centeral star forms indicates the formation and growth of planetesmals. The planetesmals produces empty rings in the disk where the growing condensations sweep up smaller particles and incorporate them. The process continues until all the available matter has been incorporated into the nearest planetesmal. Slowly the disk is depleted into larger and larger planetesmals, which untimately become the planets.
OH of planetesmal growth
The disk will have a steep temperature gradient which limits what elements can condense at any radius in the disk.
OH of Disk Temp Gradient
This scenerio accounts in a natural way for:
1. Small, rocky, metal rich inner planets (less matter near the Sun)
2. Absence of volatile elements (H, He) in the inner solar system.
3. Prograde rotation and revolution of planets and satellites
4. Co-planar orbits of the planets
5. Massive outer planets composed mostly of H & He (similar comp to that of the sun)
6. Most angular momentum in the outer planets (Jupiter and Saturn mostly)
 |
|
University of Wisconsin Fusion Technology Institute · 439 Engineering Research Building · 1500 Engineering Drive · Madison WI 53706-1609 · Telephone: (608) 263-2352 · Fax: (608) 263-4499 · Email: fti@engr.wisc.edu |
Copyright © 2003 The Board of
Regents of the University of Wisconsin System.
For feedback or accessibility issues, contact
web@fti.neep.wisc.edu.
|